Game Mechanism of the Week [Neo-Redux] 3: Bell Curves and Straight Lines
We could blame Apocalypse World for the resurgence of games that use "2d6+Modifier" as a core mechanism...But that's probably a bit harsh. The notion of rolling a pair of dice (or a trio) ad adding up the results before applying a modifier has been around for decades. I toyed around with it when I was in high school because it seemed to "work better" but I didn't know why.
With a bit more perspective, I can start to see why it seems to work better than a "flat die+modifier", or at least better in certain situations.
It's all about statistics. I'm not going to get too heavily into it, there are plenty of bloggers who've analysed this notion in deep complexity over the years.
While I've called this weekly game mechanism Bell Curves and Straight Lines, I'm mostly focusing o the pros and cons of the bell curve (not the straight lines).
Description:
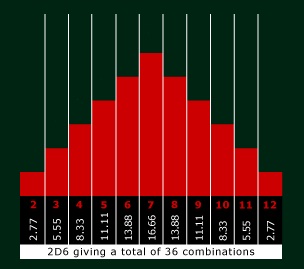
When a die is rolled, there is theoretically an even chance of getting any result offered by that die. A d6 has six options that each have a 1-in-6 chance of arising, a d12 has twelve options that each have a 1-in-12 chance of arising. When we simply add the total result of two dice together, the results vary their distribution.
On 2d6...
...there is a better chance of getting a total result of a 7 (6 chances in 36), and only a small chance of rolling a 2 or a 12 (1 chance each in 36). It's not a true bell curve,
On 3d6...
...there is still a better chance of rolling those middle values, but now there is an even lower chance of rolling the outliers of the curve (the 3 and the 18).
It's really interesting that at the fundamental level, D&D uses 3d6 to generate attributes for characters in an attempt to get a statistically "realistic" overview (most people tend toward the middle but there are chances you might be really good in one area, or really bad)....but then it uses a flat die result when testing these values (in some versions it might be to roll a d20 and compare it to your attribute, in other versions those attributes might apply a modifier to a d20 roll). In most games it's typical for a naturally high result to be an automatic success, and a naturally low result to be an automatic failure.
First consider the 2d6 (rolling 2 six-sided dice and adding the total...a vague bell curve) as a roll versus 1d12 (a straight line) as a roll. A bonus of +1 in each is a small benefit, a bonus of +3 is moderate and a bonus of +5 is quite substantial (possibly a reason while the "Apocalypse World"-derived games seem to stop at +4 as a maximum benefit).
If an action has a target number of 7 which must be met for a degree of success...
1d12 = 6 in 12 (50%) chance of success
1d12+1 = 7 in 12 (58%) chance of success
1d12+3 = 9 in 12 (75%) chance of success
1d12+5 = 11 in 12 (92%) chance of success
2d6 = 21 in 36 (58%) chance of success
2d6+1 = 26 in 36 (72%) chance of success
2d6+3 = 33 in 36 (92%) chance of success
2d6+5 = Only fail due to a naturally low roll of snake eyes: 35 in 36 (97%) chance of success.
If a harder action has a target number of 10 which must be met for a degree of success...
1d12 = 3 in 12 (25%) chance of success
1d12+1 = 4 in 12 (33%) chance of success
1d12+3 = 6 in 12 (50%) chance of success
1d12+5 = 8 in 12 (67%) chance of success
2d6 = 6 in 36 (16%) chance of success
2d6+1 = 10 in 36 (28%) chance of success
2d6+3 = 21 in 36 (58%) chance of success
2d6+5 = 30 in 36 (83%) chance of success
The range of possible die results is very similar but the modifiers make a more dramatic difference in the 2d6 version.
This becomes even more extreme when looking at a 3d6 version of the die rolls compared to a flat d20 result.
Pros:
A good bell curve gives consistency in a story, but allows for the off chance that something incredible might happen (for the good or bad). It provides the benefits of keeping numbers manageable, which is something that percentile games often have trouble with, a 1% bonus often doesn't mean a lot in a percentile game, but a bonus of +1 in a 3d6 bell curve has more significance. Conversely, a natural high in a percentile game is a 1-in-100 result, while it is a 1-in-216 result on a 3d6 bell curve.
The other immediate advantage of using multiple dice to generate a bell curve effect merely comes as a side effect of having a dice pool. Now you can apply multiple ways of reading the results...for example; rolled doubles and triples might manifest special effects, dice can be allocated to different effect results (total result determines chance of success, high die determines any unexpected benefits, low die determines any unexpected complications). I could write more about dice pools, but that's an entirely different mechanism for another week.
Cons:
I think that one of the biggest cons with the bell curve is that fact that a lot of interesting story happens among the statistical outliers. By it's very nature, the bell curve you more results at the centre and less results among the outliers.
Another con might be the fact that it takes a bit more time to add up the results of multiple dice, but in the scheme of things this is pretty negligible. Besides, "Fudge dice" are a common way to produce bell curve results at the moment, and they don't use numbers at all.
Response:
As another point, I don't know if this is really a pro or a con, I guess it all depends on the style of game you are going for. If you want modifiers to play a more important role in your game, then a bell curve will magnify their effect without the need to actually modify the numbers, thus it could be considered a pro. If you want randomness to play a bigger role in the mechanisms behind the story, then this counts as a con.
With a bit more perspective, I can start to see why it seems to work better than a "flat die+modifier", or at least better in certain situations.
It's all about statistics. I'm not going to get too heavily into it, there are plenty of bloggers who've analysed this notion in deep complexity over the years.
While I've called this weekly game mechanism Bell Curves and Straight Lines, I'm mostly focusing o the pros and cons of the bell curve (not the straight lines).
Description:
When a die is rolled, there is theoretically an even chance of getting any result offered by that die. A d6 has six options that each have a 1-in-6 chance of arising, a d12 has twelve options that each have a 1-in-12 chance of arising. When we simply add the total result of two dice together, the results vary their distribution.
On 2d6...
On 3d6...
It's really interesting that at the fundamental level, D&D uses 3d6 to generate attributes for characters in an attempt to get a statistically "realistic" overview (most people tend toward the middle but there are chances you might be really good in one area, or really bad)....but then it uses a flat die result when testing these values (in some versions it might be to roll a d20 and compare it to your attribute, in other versions those attributes might apply a modifier to a d20 roll). In most games it's typical for a naturally high result to be an automatic success, and a naturally low result to be an automatic failure.
First consider the 2d6 (rolling 2 six-sided dice and adding the total...a vague bell curve) as a roll versus 1d12 (a straight line) as a roll. A bonus of +1 in each is a small benefit, a bonus of +3 is moderate and a bonus of +5 is quite substantial (possibly a reason while the "Apocalypse World"-derived games seem to stop at +4 as a maximum benefit).
If an action has a target number of 7 which must be met for a degree of success...
1d12 = 6 in 12 (50%) chance of success
1d12+1 = 7 in 12 (58%) chance of success
1d12+3 = 9 in 12 (75%) chance of success
1d12+5 = 11 in 12 (92%) chance of success
2d6 = 21 in 36 (58%) chance of success
2d6+1 = 26 in 36 (72%) chance of success
2d6+3 = 33 in 36 (92%) chance of success
2d6+5 = Only fail due to a naturally low roll of snake eyes: 35 in 36 (97%) chance of success.
If a harder action has a target number of 10 which must be met for a degree of success...
1d12 = 3 in 12 (25%) chance of success
1d12+1 = 4 in 12 (33%) chance of success
1d12+3 = 6 in 12 (50%) chance of success
1d12+5 = 8 in 12 (67%) chance of success
2d6 = 6 in 36 (16%) chance of success
2d6+1 = 10 in 36 (28%) chance of success
2d6+3 = 21 in 36 (58%) chance of success
2d6+5 = 30 in 36 (83%) chance of success
The range of possible die results is very similar but the modifiers make a more dramatic difference in the 2d6 version.
This becomes even more extreme when looking at a 3d6 version of the die rolls compared to a flat d20 result.
Pros:
A good bell curve gives consistency in a story, but allows for the off chance that something incredible might happen (for the good or bad). It provides the benefits of keeping numbers manageable, which is something that percentile games often have trouble with, a 1% bonus often doesn't mean a lot in a percentile game, but a bonus of +1 in a 3d6 bell curve has more significance. Conversely, a natural high in a percentile game is a 1-in-100 result, while it is a 1-in-216 result on a 3d6 bell curve.
The other immediate advantage of using multiple dice to generate a bell curve effect merely comes as a side effect of having a dice pool. Now you can apply multiple ways of reading the results...for example; rolled doubles and triples might manifest special effects, dice can be allocated to different effect results (total result determines chance of success, high die determines any unexpected benefits, low die determines any unexpected complications). I could write more about dice pools, but that's an entirely different mechanism for another week.
Cons:
I think that one of the biggest cons with the bell curve is that fact that a lot of interesting story happens among the statistical outliers. By it's very nature, the bell curve you more results at the centre and less results among the outliers.
Another con might be the fact that it takes a bit more time to add up the results of multiple dice, but in the scheme of things this is pretty negligible. Besides, "Fudge dice" are a common way to produce bell curve results at the moment, and they don't use numbers at all.
Response:
As another point, I don't know if this is really a pro or a con, I guess it all depends on the style of game you are going for. If you want modifiers to play a more important role in your game, then a bell curve will magnify their effect without the need to actually modify the numbers, thus it could be considered a pro. If you want randomness to play a bigger role in the mechanisms behind the story, then this counts as a con.
.png)
Comments